Tal y como lo hemos hecho hasta ahora, en este nuevo post, el primero del 2016, continuamos con una de las tres principales partes de la exploración sismológica, el procesado de datos sísmicos, el cual en si mismo es un tema bastante extenso, por lo que en esta entrada solo daremos una breve introducción. Antes de pasar a lo que compete a este post, si no han leído las entradas anteriores pueden hacerlo dándole clic a los siguientes links:
Definición.
El procesamiento de datos sísmicos se puede definir como la alteración de datos sísmicos para suprimir ruido, mejorar la señal y migrar los eventos sísmicos a su posición apropiada en el espacio.
| Ejemplo de procesado sísmico. |
*Esta figura da una visión general de cómo se ven los datos antes y después de la secuencia de procesado. Asimismo la figura c muestra un mapa de atributo sísmico representando la velocidad de la onda a una profundidad particular del estudio sísmico. Diferentes tipos de rocas tienen diferentes velocidades, por lo que la velocidad es un buen indicador al buscar por un tipo específico de rocas. En este caso, las bajas velocidades (en azul) son características de las arenas, en este ejemplo de una antiguo cauce de río, las cuales son porosas y típicamente buenas almacenadoras de hidrocarburos.
Introducción a los fundamentos del procesado de señales.
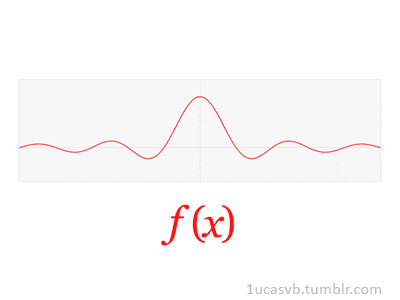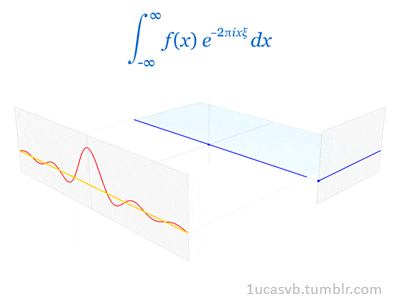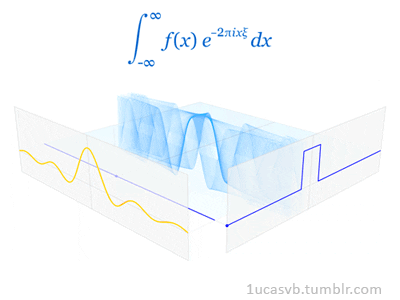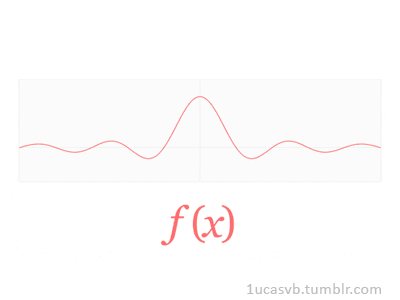
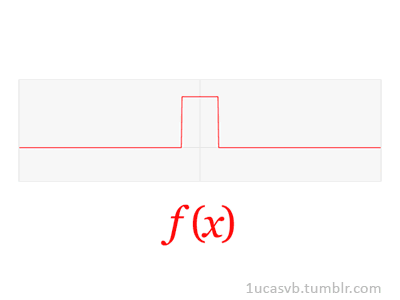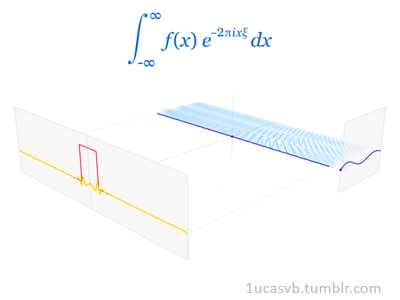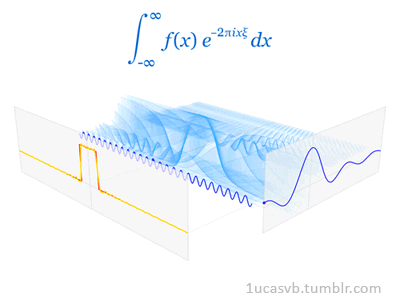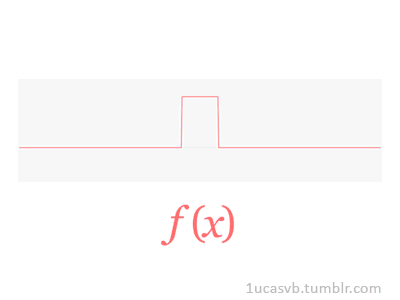
En el procesado de señales, especialmente en el análisis de datos sísmicos, la transformada de Fourier es fundamental y se aplica a casi todas las etapas de procesamiento. Una traza sísmica representa un campo de onda sísmico grabado en una posición receptora. La forma digital de una traza sísmica es una serie de tiempo la cual puede ser completamente descrita como una suma discreta de un número de sinusoides - cada uno con una amplitud pico, frecuencia, y fase. El análisis de una traza sísmica en sus componentes sinusoidales se logra a través de la transformada directa de Fourier. Inversamente, la síntesis de una traza sísmica desde sus componentes sinusoidales individuales se logra a través de la transformada inversa de Fourier.
Los algoritmos de procesado de datos sísmicos pueden ser comúnmente descritos o implementados más fácilmente en el dominio de la frecuencia que en el dominio del tiempo. Muchas de las técnicas de procesado involucran un operando (traza sísmica) y un operador (filtro). Una de las aplicaciones simples del análisis de Fourier es el diseño de filtros de frecuencia de fase cero, comúnmente en la forma de filtros pasabanda.
Algo de humor...
La transformada de Fourier en 2D es una manera de descomponer un campo de onda sísmico, tal como un gather de tiro común, en sus componentes de onda plana, cada uno con una cierta frecuencia propagándose a un cierto ángulo de la vertical. Por lo tanto, la transformada de Fourier en 2D puede describir procesos como la migración y el filtrado de frecuencia-número de onda (f-k).
| ... algo más |
Los datos sísmicos comúnmente necesitan una aplicación de una función de ganancia (escalamiento de amplitudes variante en el tiempo), por varias razones. La función de escalamiento comúnmente se deriva de los datos. En las etapas tempranas del procesado la ganancia se aplica para corregir por divergencia esférica (decaimiento de las amplitudes debido al esparcimiento geométrico de las ondas sísmicas). A los datos sísmicos se les aplica ganancia generalmente para propósitos de visualización, por ejemplo, al aplicar el control automático de ganancia (AGC por sus siglas en inglés), el cual aumenta las zonas de reflexiones débiles en los datos sísmicos. Sin embargo, una ganancia de tipo AGC puede destruir el carácter de la señal y debe, por lo tanto, ser considerada con precaución.
| Control de ganancia. En los ejemplos de la imagen se puede distinguir fácilmente la diferencia entre una sección sin y con ganancia. |
Existen tres tipos de etapas primarias en el procesamiento de datos sísmicos; cada una esta direccionada a mejorar la resolución sísmica (habilidad para separar dos eventos que están muy cerca el uno del otro) ya sea espacial o temporalmente:
1.- La deconvolución se realiza junto al eje de tiempo para incrementar la resolución temporal al comprimir la ondícula sísmica básica a aproximadamente un pico y suprimir trenes de ondas reverberantes.
| Ejemplificación del resultado de aplicar la deconvolución a una respuesta sísmica |
2.- El apilamiento, que comprime la dimensión del offset, por lo tanto reduciendo el volumen de datos sísmicos al plano de la sección sísmica de cero offset e incrementando la relación señal-ruido.
Apilamiento sísmico es básicamente la suma de las trazas.
3.- La migración es comúnmente implementada en la sección apilada (la cual se asume que es equivalente a una sección de offset cero) para incrementar la resolución lateral al colapsar las difracciones y mover los eventos buzantes a sus supuestas verdaderas posiciones en el subsuelo.
| Se muestra a) estructura en profundidad, b) sección en tiempo y c) la diferencia del resultado con la sección migrada |
Procesos secundarios son implementados en ciertas etapas para condicionar los datos y mejorar el desempeño de la deconvolución, apilamiento, y migración, pero eso lo veremos en entradas futuras y con un poco más de tiempo.
Hasta pronto!
¿Tienes algún tema que te gustaría que tratáramos? Danos like y háznoslo saber en nuestra página de Facebook, o agréganos como amigos en Facebook o Twitter.
No hay comentarios.:
Publicar un comentario